Nejslavnější matematická čísla π, Ф a e
Číslo π
π je poměr obvodu kruhu k jeho průměru. Nejstarší písemně doložené odhady π se datují do doby okolo 1900 př. n. l.; jsou to 256/81 (Egypt) a 25/8 (Babylon), oba méně než 1 % vzdálené od skutečné hodnoty.Archimédés (287–212 př. n. l.) byl první, kdo odhadl π důsledně. Uvědomil si, že hodnota může být ohraničena shora i zespoda vepsáním a opsáním pravidelných mnohoúhelníků do kružnice a vypočtením jejich obvodů. Použitím 96úhelníků dokázal, že 223/71 < π < 220/70. Průměr těchto hodnot je zhruba 3,14185.
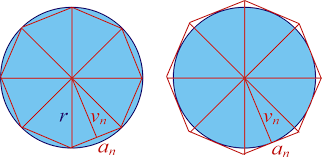
Číslu π se také říká Ludolfovo číslo, protože německý matematik 16. stokletí Ludolph van Ceulen strávil značnou část svého života počítáním jeho číselné hodnoty. Používal při tom stejné metody jako Archimédés o dva tisíce let dříve. V roce 1596 publikoval hodnotu čísla π s přesností na 20 desetinných míst, později výpočet zpřesnil na 35 desetinných míst (s pravidelným mnohoúhelníkem o 262 stranách).
Číslo Ф bylo vysvětleno v kapitole o zlatém řezu.
Číslo e
Eulerovo číslo e objevil roku 1683 Jacob Bernoulli při zkoumání složeného úročení: Eulerovo číslo je totiž limitní roční návratnost jednotkové částky při ročním stoprocentním úroku, pokud se frekvence splácení zvyšuje nade všechny meze.Přibližná hodnota Eulerova čísla je 2,71828182846.
Představme si, že máme jednu korunu, kterou dáme do banky, která nám nabízí 100% roční úrok. Kolik peněz budeme mít na účtu přesně po roce? Budeme mít 2 koruny.
Jak by se situace změnila, kdyby nám banka nabídla 50% úrok, který by se úročil co půl roku? Bylo by to pro nás výhodnější, nebo méně výhodné?
Po prvním půl roce bychom měli o polovinu více, tedy 1 + 1/2 = 1,5
Po druhém půl roce bychom měli zase o další polovinu více: 1,5 * (1 + 1/2) = 2,25
Po roce tak máme na účtě 2,25 korun. Častější úročení nižším úrokem je tedy pro nás výhodné.
Co kdyby nám banka nabízela úročení každý měsíc, ale úrok by klesl na jednu dvanáctinu původního úroku?
Za první měsíc získáme 1 + 1/12 = 1,08333
Budeme-li pokračovat stejně, dostaneme (1 + 1/12)12 = 2,6130352
Kdybychom úročili každý den, dostaneme (1 + 1/365)365 = 2,7145674
Takhle bychom mohli pokračovat do nekonečna - úročit každou minutu, každou sekundu, každou milisekundu, každou nanosekundu… až bychom se dostali do stavu, že úročíme neustále. Kolik bychom v takovém případě měli po roce na účtě peněz?
To je otázka, kterou se Jacob Bernoulli snažil vypočítat.
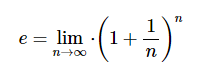
Bohužel to ale nedokázal a dokázal to až v 18. století švýcarský matematik Leonhard Euler. Ten spočítal, že po roce bychom měli na účtu přibližně 2,71828182846 korun.
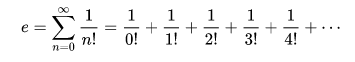
Eulerova rovnost neboli vztah mezi čísly π a e
Euler navíc dokázal, že mezi nejslavnějšími matematickými konstantami existuje jednoduchý vztah:eiπ + 1 = 0
Eulerova rovnost dává do souvislosti tři základní aritmetické operace (součet, součin a mocnina) s pěti základními analytickými konstantami (e, i, π, 0, 1) a je proto považována za jeden z nejvýznamnějších matematických vztahů vůbec.
(1707 - 1783)
Leonhard Paul Euler byl švýcarský matematik a fyzik. Je považován za nejlepšího matematika 18. století a za jednoho z nejlepších matematiků vůbec.